Table des matières
L.O.L. - Liège OpenSCAD Library
Le code est ici : L.O.L. - Code
Créée par Marc Vanlindt - CC-BY-SA Belgique 2.0
Le but de cette librairie est de faire en sorte que toutes les primitives 2D puissent être appelées en tant que variables.
Plusieurs fonctions et modules ont donc été réalisés pour les créer mais également pour en créer de nouvelles et les modifier plus en profondeur.
Une fois les primitives utilisées en tant que variables, il est possible d'y appliquer des modifications en principe accessibles qu'aux polygones ou aux vecteurs, ces formes étant les seules dont il est possible de retirer les coordonnées de chaque point le composant.
Attention :
- Toutes les fonctions présentes dans la librairie n'ont pas encore été documentées, certaines d'entre elles ayant encore quelques bugs.
- Beaucoup de fonctions font appels à d'autres fonction de la librairie, il vaut mieux donc l'utiliser “en entier”.
- En réalisant cet article, je me suis rendu compte de certaines erreurs corrigées dans le code source, mais pas forcément dans le wiki.
- Certaines fonctions nécessitent d'avoir la version la plus récente possible de OpenSCAD.
- Il y a de nombreuses erreurs pouvant apparaître dans la console si vous l'enclenchez. C'est “normal”! (Enfin non, ça ne l'est pas, mais ça fonctionne quand même ^^)
- Merci d'utiliser la dernière version et, si possible, la version “Development Snapshots” : https://openscad.org/downloads.html#snapshots
Variables générales
LogoFB= [[4.46567, 4.99666], [3.06433, 4.99666], [3.06433, 0], [0.987666, 0], [0.987666, 4.99666], [0, 4.99666], [0, 6.76134], [0.987666, 6.76134], [0.987666, 7.90467], [1.00769, 8.22956], [1.07504, 8.57716], [1.20063, 8.92712], [1.39537, 9.25909], [1.6702, 9.55271], [2.03602, 9.78764], [2.50376, 9.94352], [3.08433, 10], [4.62167, 9.99402], [4.62167, 8.28068], [3.505, 8.28068], [3.35933, 8.26038], [3.21662, 8.18648], [3.10811, 8.0397], [3.065, 7.80073], [3.065, 6.76073], [4.64833, 6.76073]]; LetterL=[[0,0],[0,70],[22,73],[19,21],[50,25],[48,-1],[0,0]]; LetterO=[[0,35],[6.25,61.25],[25,70],[25,70],[43.75,61.25],[50,35],[50,35],[43.75,8.75],[25,0],[25,0],[6.25,8.75],[0,35]]; blue = [0,0,1,1]; red = [1,0,0,1]; green = [0,1,0,1]; violet = [0.5,0,0.5,1]; yellow = [1,1,0,1]; cyan = [0,1,1,1]; black = [0,0,0,1]; white = [1,1,1,1]; oak = RVB(200,50,90,255); orange = [1,0.5,0,1]; olive = [0.5,0.5,0,1]; sarcelle = [0,0.5,0.5,1]; marine = [0,0,0.5,1]; fuschia = [1,0,1,1]; glass = [1,0,1,0.2]; bleu = [0,0,1,1]; rouge = [1,0,0,1]; vert = [0,1,0,1]; jaune = [1,1,0,1]; noir = [0,0,0,1]; blanc = [1,1,1,1]; gris = [0.5,0.5,0.5,1]; gray = [0.5,0.5,0.5,1]; pink = RVB(255,107,219,255); rose = RVB(255,107,219,255); phi = 1.61803399; aphi = phi-1; biphi = phi+1; angledor = 360/biphi; py = sqrt(0.5); bipy = sqrt(2); pi = 3.141592654; tau = pi*2;
Fonctions de base
2D(a) et 3D(a)
abc=square(); def=cube(); 2D(abc); translate([11,0,0]) 3D(def);
module 2D(a){
polygon(a);
}
module 3D(a){
if(a[1]!=undef)
{
polyhedron(a[0],a[1]);
}
}
Nouvelles fonctions sur nombres
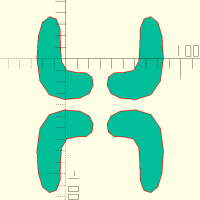
random(n,s,pos)
Donne un nombre aléatoire entre 0 et n si pos est sur *true* (par défaut) et entre -n et n si pos est sur *false*. s correspond à la valeur utilisée pour générer le nombre aléatoire. 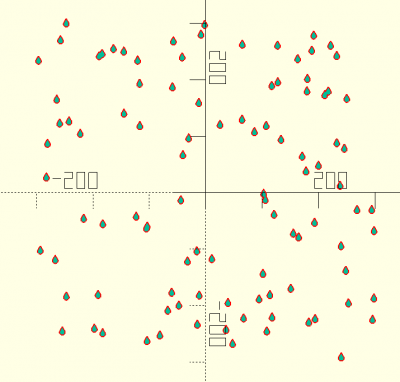
for(i=[1:100]){
translate([random(n=300,s=i,pos=false),random(n=300,s=i*2,pos=false)]) teardrop();
}
function random (n,s,pos) = rands(pos==undef?0:pos==true?0:-n,n,1,s==undef?n:s)[0];
hypo(a,b)
Donne l'hypothénuse en fonction de deux longueurs.
echo(hypo(3,4)); -> ECHO: 5
function hypo (a,b) = sqrt((a*a)+(b*b));
pair(a)
for(i=[0:10]){echo(i," : ",pair(i));}
-> ECHO: 0, " : ", true
ECHO: 1, " : ", false
ECHO: 2, " : ", true
ECHO: 3, " : ", false
ECHO: 4, " : ", true
ECHO: 5, " : ", false
ECHO: 6, " : ", true
ECHO: 7, " : ", false
ECHO: 8, " : ", true
ECHO: 9, " : ", false
ECHO: 10, " : ", true
function pair (a) = a%2==0?true:false;
normal(a)
abc=[[0,0],[100,100]]; echo(normal(abc)); -> ECHO: [[0, 0], [0.707107, 0.707107]]
function normal (a) = a/(sqrt(a[0]*a[0]+a[1]*a[1]));
ppcm(a,b,q)
abc=ppcm(10,25); def=ppcm(11,17); ghi=ppcm(32,24); echo(abc); echo(def); echo(ghi); ->ECHO: [5,2] -> 5*10 = 2*25 ECHO: [17,11] -> 17*11 = 11*17 ECHO: [3,4] -> 3*32 = 4*24
function ppcm(a,b,q)=let( aa=[for(i=[0:max(a,b)]) each [i*a*(q==undef?1:q)]], bb=[for(i=[0:max(a,b)]) each [i*b*(q==undef?1:q)]], cc=[for(i=[0:max(a,b)]) each [for(j=[1:100]) each aa[i]==bb[j]?bb[j]:""]]) [cc[0]/a,cc[0]/b];
Nouvelles fonctions sur les tables
abc=[10,2,9,7,5,6,4,8,3,1];
echo("sum :", sum(abc));
echo("topct :", topct(abc));
echo("moyenne :", moyenne(abc));
echo("invert :", invert(abc));
echo("sort :", sort(abc));
-> ECHO: "sum :", 55
ECHO: "topct :", [0.181818, 0.0363636, 0.163636, 0.127273, 0.0909091, 0.109091, 0.0727273, 0.145455, 0.0545455, 0.0181818]
ECHO: "moyenne :", 5.5
ECHO: "invert :", [1, 3, 8, 4, 6, 5, 7, 9, 2, 10]
ECHO: "sort :", [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
function sum (a,b=0,c=0,n) = b<(n==undef?len(a):n)?sum(a=a,b=b+1,c=c+a[b],n=n):c;
function topct (a) = a/sum(a);
function moyenne (a,b=0,c=0) = b<len(a)?sum(a=a,b=b+1,c=c+a[b])/len(a):c;
function invert (a) = let(b=[for(i=[0:len(a)-1]) a[(len(a)-1)-i]])b;
function sort (a,invert=false) = len(a) == 0 ? [] : let (
b=floor(len(a)/2),
c=[for(i=a) if (i<a[b]) i],
d=[for(i=a) if (i>a[b]) i],
e=[for(i=a) if (i==a[b]) i]
)
invert==false?concat(sort(c),e,sort(d)):invert(concat(sort(c),e,sort(d)));
Nouvelles fonctions sur les vecteurs
length(a,b)
Retourne la longueur entre deux points.
abc=[100,100]; def=[200,200]; echo(length(abc,def)); -> ECHO: 141.421
function length (a,b) = sqrt(((b[0]-a[0])*(b[0]-a[0]))+((b[1]-a[1])*(b[1]-a[1])));
divide(a,b,c)
abc=[50,50]; def=[100,100]; ghi=[for(i=[0:10])divide(abc,def,i/10)]; echo(ghi); -> ECHO: [[50, 50], [55, 55], [60, 60], [65, 65], [70, 70], [75, 75], [80, 80], [85, 85], [90, 90], [95, 95], [100, 100]]
function divide(a,b,c) = [a[0]+(b[0]-a[0])*c, a[1]+(b[1]-a[1])*c];
addpoints(a,b,n)
Attention : pour les besoins que j'en ai eu, cette fonction ne “ferme” pas la forme et seul le premier point est inclus, non le dernier!
abc=[50,50]; def=[100,100]; jkl=addpoints(abc,def,5); echo(jkl); -> ECHO: [[50, 50], [58.3333, 58.3333], [66.6667, 66.6667], [75, 75], [83.3333, 83.3333], [91.6667, 91.6667]]
function addpoints(c1,c2,n)=[for(i=[0:n]) each [divide(c1,c2,i/(n+1))]];
myangle(a,b)
abc=[0,0]; def=[100,100]; echo(myangle(abc,def)); ->ECHO: 45
function myangle(a,b) = atan2(b[0]-a[0],b[1]-a[1]);
join(a) - join2(a)
Join2 n'est pas compatible avec toutes les versions de OpenSCAD.
abc=[0,0]; def=[100,100]; ghi=[200,200]; jkl=[300,300]; echo(join([abc,def,ghi,jkl])); echo(join2([abc,def,ghi,jkl])); ->ECHO: [0, 0, 100, 100, 200, 200, 300, 300] ECHO: [0, 0, 100, 100, 200, 200, 300, 300]
function join(a,c=0,t=[]) = let (u=concat(t,a[c]))c==len(a)?t:join(a=a,c=c+1,t=u); function join2(aa) = [for(i=[0:len(aa)-1] ) each aa[i]];
clean(a)
abc=[[0,0],[1,1],undef,[2,2],[2,2],[3,3],undef,[4,4],[5,5],[5,5]]; echo(clean(abc)); -> ECHO: [[0, 0], [1, 1], [2, 2], [3, 3], [4, 4], [5, 5]]
function clean(a) = [for(i=[0:len(a)-1]) each (a[i]==a[i+1]?"":a[i][0]==undef?"":[a[i]])];
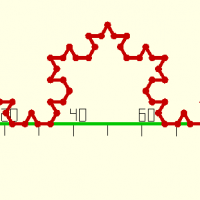
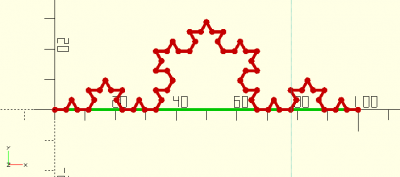
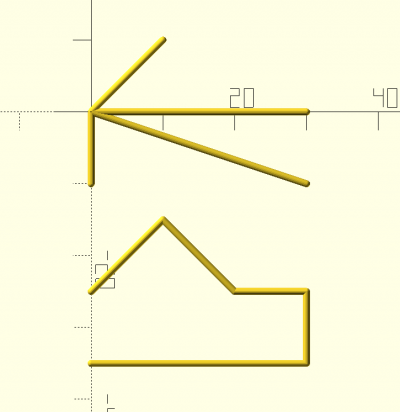
fract(a,angle,maxit,close)
abc=[[0,0],[100,0]]; def=fract(abc,in=false,angle=60,maxit=3,close=false); echo(def); color(vert) trace(abc); color(rouge) trace(def); ->ECHO: [[0, 0], [3.7037, 0], [5.55556, 3.2075], [7.40741, 0], [11.1111, 0], [12.963, 3.2075], [11.1111, 6.415], [14.8148, 6.415], [16.6667, 9.6225], [18.5185, 6.415], [22.2222, 6.415], [20.3704, 3.2075], [22.2222, 0], [25.9259, 0], [27.7778, 3.2075], [29.6296, 0], [33.3333, 0], [35.1852, 3.2075], [33.3333, 6.415], [37.037, 6.415], [38.8889, 9.6225], [37.037, 12.83], [33.3333, 12.83], [35.1852, 16.0375], [33.3333, 19.245], [37.037, 19.245], [38.8889, 22.4525], [40.7407, 19.245], [44.4444, 19.245], [46.2963, 22.4525], [44.4444, 25.66], [48.1481, 25.66], [50, 28.8675], [51.8519, 25.66], [55.5556, 25.66], [53.7037, 22.4525], [55.5556, 19.245], [59.2593, 19.245], [61.1111, 22.4525], [62.963, 19.245], [66.6667, 19.245], [64.8148, 16.0375], [66.6667, 12.83], [62.963, 12.83], [61.1111, 9.6225], [62.963, 6.415], [66.6667, 6.415], [64.8148, 3.2075], [66.6667, 0], [70.3704, 0], [72.2222, 3.2075], [74.0741, 0], [77.7778, 0], [79.6296, 3.2075], [77.7778, 6.415], [81.4815, 6.415], [83.3333, 9.6225], [85.1852, 6.415], [88.8889, 6.415], [87.037, 3.2075], [88.8889, 0], [92.5926, 0], [94.4444, 3.2075], [96.2963, 0], [100, 0]]
function fract(a,angle,in,maxit,it,close)= let(
close=close==undef?true:close,
a=close==true?a[0]==a[len(a)-1]?a:concat(a,[a[0]]):a,
maxit=maxit==undef?3:maxit==0?1:maxit,
it=it==undef?0:it,
inside=in==undef?1:in==true?1:-1,
angle=angle==undef?60:angle,
b = [ for ( i = [ 0 : len(a)-2 ] ) [
a[i],
divide(a[i],a[i+1],angle/180),
divide(a[i],a[i+1],angle/180) +
[
sin(myangle(a[i],a[i+1]) + angle*inside) * (length(a[i],a[i+1])/3) ,
cos(myangle(a[i],a[i+1]) + angle*inside) * (length(a[i],a[i+1])/3)
],
divide(a[i],a[i+1],1-(angle/180)),
a[i+1]]
]
)
it+1==maxit?clean(join2(b)):fract(a=clean(join2(b)),angle=angle,in=in,maxit=maxit,it=it+1,close=close);
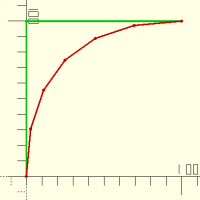
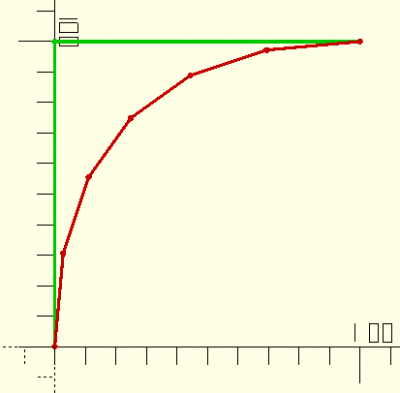
curve(table,fn)
abc=[[0,0],[0,100],[100,100]]; def=curve(abc,fn=6); echo(def); color(vert) trace(abc); color(rouge) trace(def); ->ECHO: [[0, 0], [2.77778, 30.5556], [11.1111, 55.5556], [25, 75], [44.4444, 88.8889], [69.4444, 97.2222], [100, 100]]
function curve(table,fn) = let(
fn = fn == undef ? 8 : fn,
c = [ for ( i = [0:(fn)] ) each [divide(table[0],table[1],1/(fn)*i)]],
d = [ for ( i = [0:(fn)] ) each [divide(table[1],table[2],1/(fn)*i)]],
e = [ for ( i = [0:(fn)] ) each [divide(c[i],d[i],1/(fn)*i)]])
e;
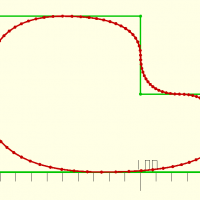
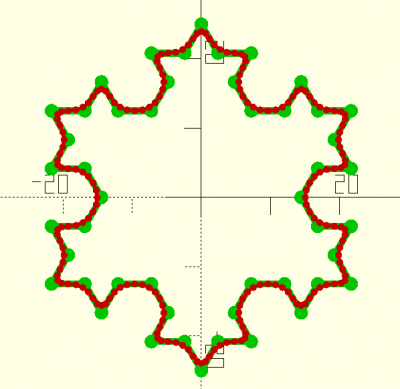
chaincurve(table,fn,closed,detail)
abc=fractshape(d=50,fn=3,maxit=2,inside=false); def=chaincurve(abc,closed=true,fn=4); echo(def); color(vert) trace(abc); color(rouge) trace(def,dot=true,d=0.5);
function chaincurve(table,fn,closed,detail) = let ( detail=detail==undef?1:detail==0?1:detail*sign(detail)*2+1, closed=closed==undef?true:closed, totaltab=concat(table,[table[0]],closed==true?[table[1]]:"",closed==true?[table[2]]:""), tab = multiplyfaces(totaltab,detail), d = [for (i=[(closed==true?4:2):2:len(tab)-(closed==false?4:2)]) each curve([tab[(i)-1],tab[i],tab[i+1]],fn)], b =table[0], c = table[len(table)-1], a = d ) clean(a);
doublevector(table,f)
abc=[[0,0],[100,0]]; for(i=[0:3])echo(doublevector(abc,f=i)); ->ECHO: [[0, 0], [50, 0], [100, 0]] ECHO: [[0, 0], [25, 0], [50, 0], [75, 0], [100, 0]] ECHO: [[0, 0], [12.5, 0], [25, 0], [37.5, 0], [50, 0], [62.5, 0], [75, 0], [87.5, 0], [100, 0]] ECHO: [[0, 0], [6.25, 0], [12.5, 0], [18.75, 0], [25, 0], [31.25, 0], [37.5, 0], [43.75, 0], [50, 0], [56.25, 0], [62.5, 0], [68.75, 0], [75, 0], [81.25, 0], [87.5, 0], [93.75, 0], [100, 0]]
function doublevector(table,f,it=0) = let(
f=f==undef?0:f,
aa = [for (i=[0:len(table)-1]) each [table[i],divide(table[i],table[i+1],1/2)]]
)
it==f?clean(aa):doublevector(clean(aa),f=f,it=it+1);
function fractalize(table,force,maxit,seed)= let (
force=force==undef?1:force,
maxit=maxit==undef?3:maxit,
seed=seed==undef?1:seed,
aa=
[
for(i=[0:len(table)-2], ab = doublevector([[table[i][0],table[i][1]],[table[i+1][0],table[i+1][1]]],f=maxit))
for(j=ab[0]) each clean([[ab][0],[ab][1]]+[[(random(pos=false,n=force,s=sin(seed)*sin(ab[0])+sin(ab[1]))),(random(pos=false,n=force,s=cos(seed)*cos(ab[0])-sin(ab[1])))],[(random(n=force,s=tan(seed)+sin(ab[0])+2*cos(ab[1]))),(random(n=force,s=cos(seed)+cos(ab[0])-3*cos(ab[1])))]])
]
)
clean(aa);
fractalize(table,force,maxit,seed)
abc=square([50,100]); def=fractalize(abc,force=1,maxit=4); ghi=chaincurve(def); 2D(def); translate([55,0,0]) 2D(ghi);
function fractalize(table,force,maxit,seed)= let (
force=force==undef?1:force,
maxit=maxit==undef?3:maxit,
seed=seed==undef?1:seed,
aa=
[
for(i=[0:len(table)-2], ab = doublevector([[table[i][0],table[i][1]],[table[i+1][0],table[i+1][1]]],f=maxit))
for(j=ab[0]) each clean([[ab][0],[ab][1]]+[[(random(pos=false,n=force,s=sin(seed)*sin(ab[0])+sin(ab[1]))),(random(pos=false,n=force,s=cos(seed)*cos(ab[0])-sin(ab[1])))],[(random(n=force,s=tan(seed)+sin(ab[0])+2*cos(ab[1]))),(random(n=force,s=cos(seed)+cos(ab[0])-3*cos(ab[1])))]])
]
)
clean(aa);
interpolate(a,b,step,maxstep,correct,q)
abc=square([10,10],center=true); def=circle(d=10,fn=7); ghi=interpolate(abc,def,step=0,maxstep=1,correct=0,q=1); jkl=interpolate(abc,def,step=1,maxstep=1,correct=0,q=1); echo(len(abc)); echo(len(def)); echo(len(ghi)); echo(len(jkl)); trace(abc,dot=true,d=0.3); translate([15,0,0]) trace(def,dot=true,d=0.3); translate([0,-15,0]) trace(ghi,dot=true,d=0.3); translate([15,-15,0]) trace(jkl,dot=true,d=0.3); ->ECHO: 5 ECHO: 8 ECHO: 29 ECHO: 29
function interpolate(a,b,step,maxstep,correct,q)= let( pp=ppcm(len(a)-1,len(b)-1,q)-[1,1], correct=correct==undef?0:correct, abc=vectranslate(multiplyfaces(a,pp[0]),n=correct==undef?0:correct), def=multiplyfaces(b,pp[1]), aa=[for(i=[0:len(def)]) each [divide(abc[i],def[i],step/(maxstep))]]) (aa);
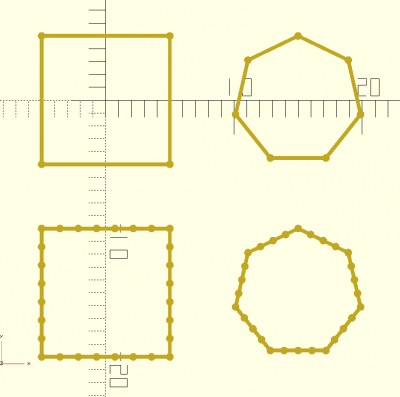
multiplyfaces(object,n)
abc=square([10,10],center=true);
echo(len(abc));
for(i=[1:4]){
def=multiplyfaces(abc,i);
echo(len(def));
translate([12*(i-1),0,0]) trace(def,d=0.3);
}
->ECHO: 5
ECHO: 9
ECHO: 13
ECHO: 17
ECHO: 21
function multiplyfaces(object,n)=let( n=n==undef?1:n==0?0:n, aa=n==0?object:[for(i=[0:len(object)-2]) each addpoints(object[i],object[i+1],n) ]) concat(clean(aa),[object[0]]);
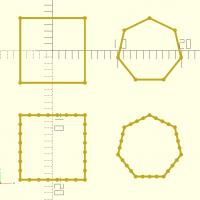
Primitives 2D
Les primitives 2D peuvent-être appellées de la même manière que celles présentes de base dans openscad.
Mais il est également possibles de faire appel à toutes sous forme de variable :
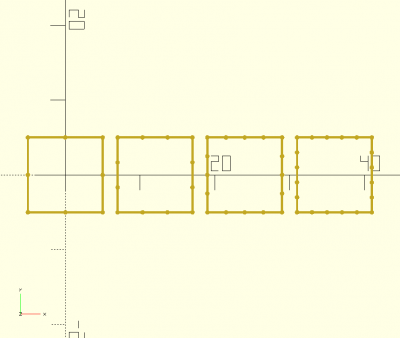
square(d,center)
abc = square([10,20],center=true); square([10,20],center=true); translate ([12,0,0]) 2D(abc);
function square(d,center)=let(
center=center==undef?false:center,
d=d==undef?[10,10]:d,
c1 = center == true ? [-d[0]/2,-d[1]/2] : [ 0, 0],
c2 = center == true ? [-d[0]/2, d[1]/2] : [ 0, d[1]],
c3 = center == true ? [ d[0]/2, d[1]/2] : [ d[0], d[1]],
c4 = center == true ? [ d[0]/2,-d[1]/2] : [ d[0], 0],
aa=[c1,c2,c3,c4,c1]
)
aa;
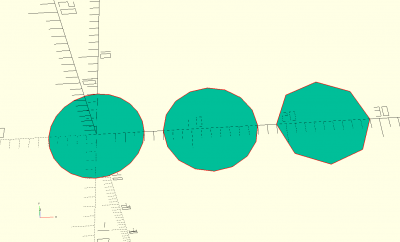
circle(d,r,fn)
abc = circle(d=10,fn=16); def = circle(r=5,fn=8); circle(d=10,$fn=24); translate ([12,0,0]) 2D(abc); translate ([24,0,0]) 2D(def);
function circle(d,r,fn) = let (
fn=fn==undef?16:fn,
r=r==undef?d==undef?5:d/2:r,
aa=ngon(d=r*2,fn=fn)
)
aa;
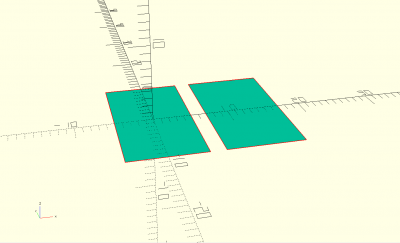
ellipse(s,fn)
abc = ellipse([40,20],fn=12); ellipse([20,40],fn=24);; translate ([40,0,0]) 2D(abc);
function ellipse(s,fn) = let (
fn=fn==undef?16:fn,
s=s==undef?[10,10*aphi]:s,
aa=[for(i =[0:fn] ) [sin(360/fn*i)*s[0],cos(360/fn*i)*s[1]]]
)
aa;
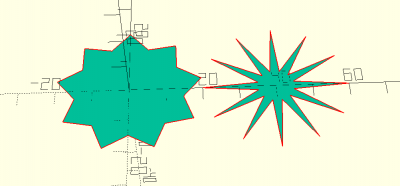
star(d1,d2,fn)
abc = star(d1=40,d2=10,fn=12); star(d1=40,d2=30,fn=9); translate ([40,0,0]) 2D(abc);
function star(d1,d2,fn) = let (
d1=d1==undef?10:d1,
d2=d2==undef?5:d2,
fn=fn==undef?7:fn,
aa=[for(i=[0:2*(fn)])[sin(360/(2*fn)*i)*(pair(i)==true?d1:d2),cos(360/(2*fn)*i)*(pair(i)==true?d1:d2)]]
)
aa;
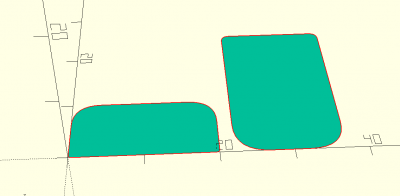
roundsquare(s,d,fn)
abc = roundsquare([15,25],[10,2.5,2.5,10]); roundsquare([20,10],[1,8,8,1]); translate ([22,0,0]) 2D(abc);
function roundsquare(s,d,fn) = let ( fn = fn == undef ? 8:fn, s = s == undef ? [15,20] : s, d = d == undef ? [3,6,3,6] : len(d) == 1 ? [d[0]/2,d[0]/2,d[0]/2,d[0]/2]:len(d)==2?[d[0]/2,d[1]/2,d[1]/2,d[1]/2]:len(d)==3?[d[0]/2,d[1]/2,d[2]/2,d[2]/2]:d[0]==undef?[d/2,d/2,d/2,d/2]:d/2, p1 = [0,0], p2 = [0,d[0]], p3 = [0,s[1]-d[1]], p4 = [0,s[1]], p5 = [d[1],s[1]], p6 = [s[0]-d[2],s[1]], p7 = [s[0],s[1]], p8 = [s[0],s[1]-d[2]], p9= [s[0],d[3]], p10= [s[0],0], p11= [s[0]-d[3],0], p12= [d[0],0], c1=curve([p3,p4,p5],fn=fn), c2=curve([p6,p7,p8],fn=fn), c3=curve([p9,p10,p11],fn=fn), c4=curve([p12,p1,p2],fn=fn), aa=clean(join2([c1,c2,c3,c4,[p3]])) ) aa;
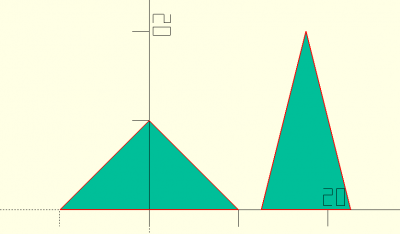
triangle(w,h)
abc = triangle(10,20); triangle(20,10); translate ([17.55,0,0]) 2D(abc);
function triangle(w,h)= let ( h=h==undef?cos(30)*w:h, aa=[[-w/2,0],[0,h],[w/2,0],[-w/2,0]] ) aa;
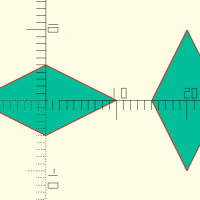
piepart(d,a,p)
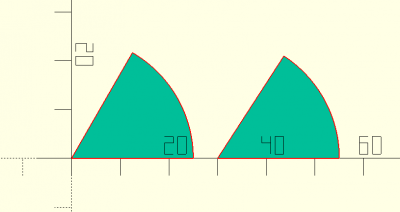 Où d est le diamètre, a un angle et p une fraction.
Où d est le diamètre, a un angle et p une fraction.
Si a et p ont tous les deux une valeurs, seul l'angle sera pris en compte.
abc=piepart(d=50,p=16/100); piepart(d=50,a=60); translate([30,0,0]) 2D(abc);
function piepart(d,a,p) = let ( d=d==undef?10:d/2, a=a==undef?p==undef?90:p>=1?360*1/p:360*p:a, aa=concat([[0,0]],[for(i=[0:a])[-sin(-90+i)*d,cos(-90+i)*d]]) ) aa;
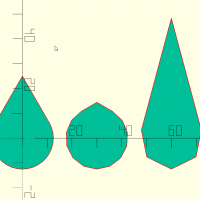
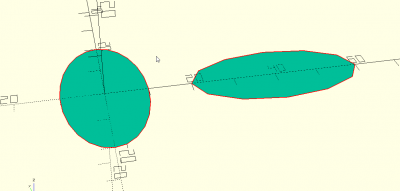
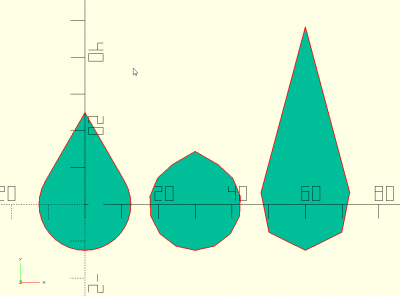
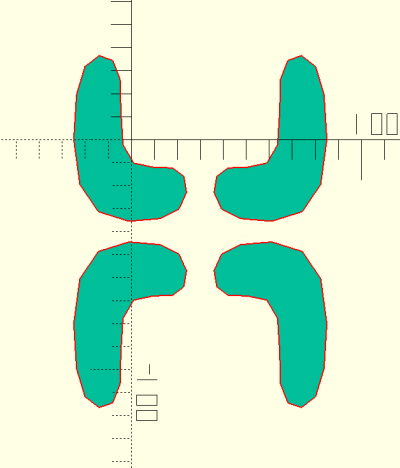
teardrop(d,a,fn)
abc=teardrop(25,60,12); def=teardrop(25,15,4); teardrop(25,30,24); translate([30,0,0]) 2D(abc); translate([60,0,0]) 2D(def);
function teardrop(d,a,fn)=let ( d=d==undef?10:d, a=a==undef?30:a, h=d*tan(90-a), fn=fn==undef?16:fn, courbe= [for(i=[0:fn]) [sin(90-a+(360-(90-a)*2)/fn*i)*d/2,cos(90-a+(360-(90-a)*2)/fn*i)*d/2]], aa=concat(courbe,[[0,(cos(90-a)*d/2)+h*sin(90-a)/2]],[[sin(90-a)*d/2,cos(90-a)*d/2]]) ) aa;
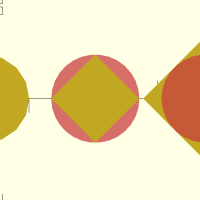
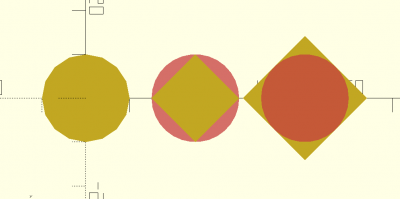
ngon(d,fn,inside)
abc=ngon(20,4,inside=true); def=ngon(20,4,inside=false); ngon(20,16); translate([25,0,0]) 2D(abc); translate([50,0,0]) 2D(def); translate([25,0,-1]) #circle(d=20); translate([50,0,1]) #circle(d=20);
function ngon(d,fn,inside) = let (
d=d==undef?10:inside==undef?d:inside==true?d:d*((d/2)/(cos(360/fn/2)*d/2)),
fn=fn==undef?4:fn,
aa=[for(i=[0:fn])[sin(360/fn*i)*d/2,cos(360/fn*i)*d/2]]
)
aa;
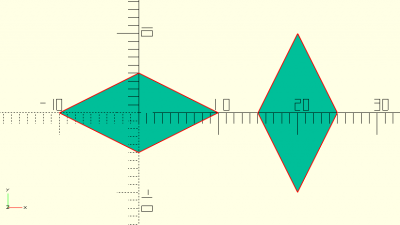
losange(dim)
abc=losange([10,20]); losange([20,10]); translate([20,0,0]) 2D(abc);
function losange(s) = let (
s=s==undef?[10,10*aphi]:s,
aa=[for(i =[0:4] ) [sin(360/fn*i)*s[0]/2,cos(360/fn*i)*s[1]/2]]
)
aa;
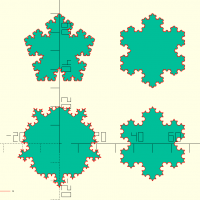
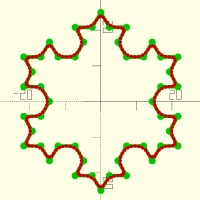
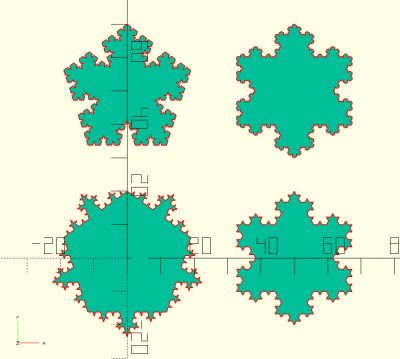
fractshape(d,fn,inside,maxit)
abc=fractshape(d=40,fn=5,it=3,inside=true); def=fractshape(d=40,fn=6,it=3,inside=true); fractshape(d=40,fn=5,it=3,inside=false); translate([50,0,0]) fractshape(d=40,fn=3,it=3,inside=false); translate([0,50,0]) 2D(abc); translate([50,50,0]) 2D(def);
function fractshape(d,fn,inside,maxit)= let( d=d==undef?10:d/2, fn=fn==undef?5:fn, maxit=maxit==undef?3:maxit, inside=inside==undef?true:inside, angle=fn==3?60:fn==4?89:360/fn, points=fract(ngon(d=d*2,fn=fn),maxit=maxit,angle=angle,in=inside) ) points;
Primitives 3D
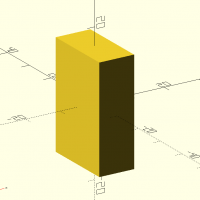
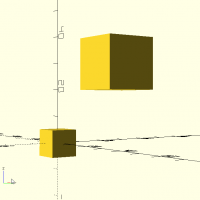
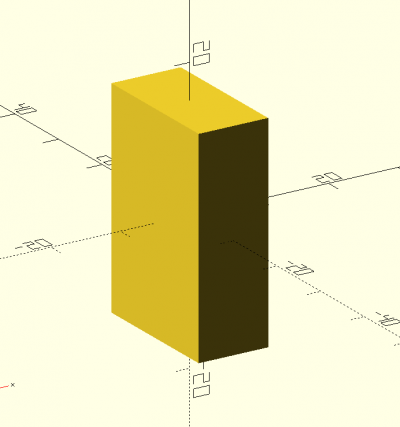
cube(d,center)
abc=cube([10,20,30],center=true); echo(abc); 3D(abc);
function cube(d,center)=let
(
d=d==undef?[10,10,10]:d,
center=center==undef?false:center,
mys=square([d[0],d[1]],center=center),
aa=to3D(mys,mys,h=d[2])
)
center==false?aa:translate3D(aa,[0,0,-d[2]/2]);
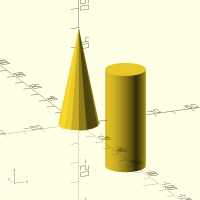
cylinder(d,d1,d2,h,fn,center)
abc=cylinder(d1=20,d2=0,h=50,fn=16); def=cylinder(d=20,h=50,fn=64,center=true); 3D(abc); translate([25,0,0]) 3D(def);
function cylinder(d,d1,d2,h,fn,center)=let
(
d1=d==undef?d1==undef?10:d1:d,
d2=d==undef?d2==undef?10:d2:d,
h=h==undef?40:h,
fn=fn==undef?16:fn,
center=center==undef?false:center,
myg1=ngon(d=d1,fn=fn),
myg2=ngon(d=d2,fn=fn),
aa=to3D(myg1,myg2,h=h)
)
center==false?aa:translate3D(aa,[0,0,-h/2]);
Divers
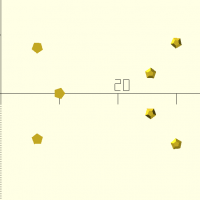
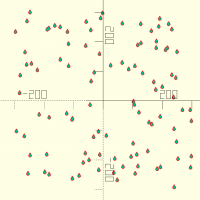
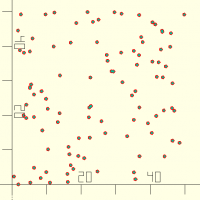
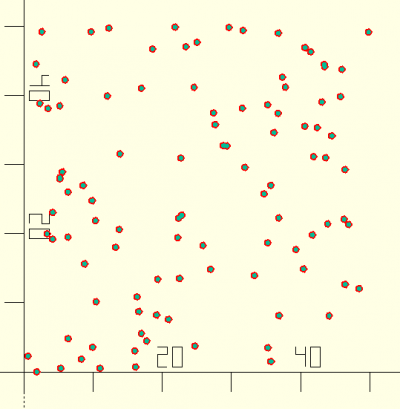
pointgrid(dim,n,seed)
abc=pointgrid([50,50],n=100); echo(abc); for(i=abc)translate(i) circle(d=1);
function pointgrid(dim,n,seed) =[for(i=[0:n-1])[random(n=dim[0],s=sin(i/n/(seed==undef?1:seed))),random(n=dim[1],s=cos(i*2/n/(seed==undef?1:seed)))]];
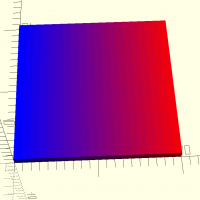
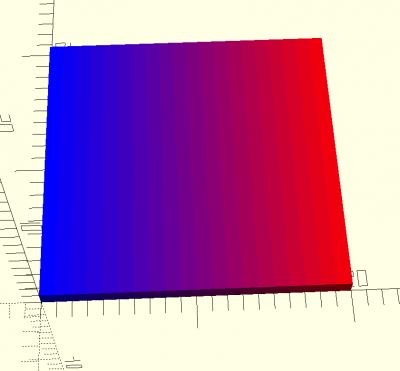
gradient (a,b,c)
abc=[0,0,1,1]; def=[1,0,0,1]; ghi=gradient(abc,def,20); for(i=[0:19]) translate([i,0,0]) color(ghi[i]) cube([1,20,1]);
function gradient(a,b,c) = let ( c=c==undef?1:c, aR=a[0], aV=a[1], aB=a[2], aA=a[3], bR=b[0], bV=b[1], bB=b[2], bA=b[3], mR=(aR-bR)/c, mV=(aV-bV)/c, mB=(aB-bB)/c, mA=(aA-bA)/c, aa=[for(i=[0:c-1]) [a[0]-mR*i,a[1]-mV*i,a[2]-mB*i,a[3]-mA*i]] ) aa;
RVB(a,b,c,d)
color(RVB(192,64,128)) cube(); translate([1.1,0,0]) color(RVB(12,64,255,128)) cube(); translate([2.2,0,0]) color(RVB(255,255,0,64)) cube();
function RVB(a,b,c,d)= let( a=a==undef?0.5:1/255*a, b=b==undef?0.5:1/255*b, c=c==undef?0.5:1/255*c, d=d==undef?1:1/255*d, aa=[a,b,c,d] )aa;
Objets 2D
Ces objets ne peuvent être appelés sous forme de variables.
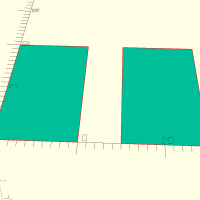
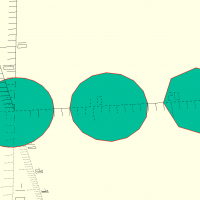
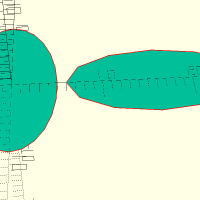
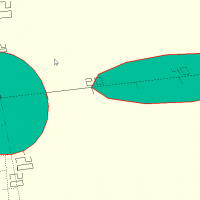
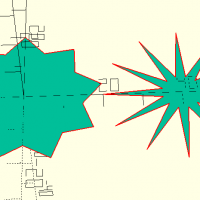
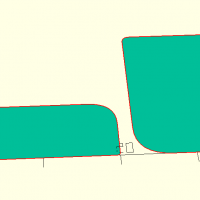
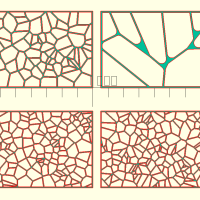
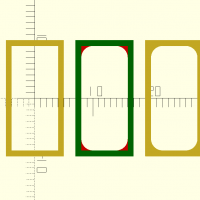
voronoi(dim, w, c, n, seed)
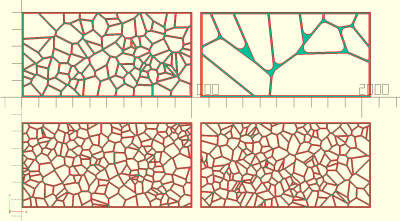 Où w est la largeur du trait, c une courbure ouvant être appliqué aux angles à l'intérieur du motif, n le nombre de cellules voules et seed la graine à utiliser pour l'aléatoire.
Où w est la largeur du trait, c une courbure ouvant être appliqué aux angles à l'intérieur du motif, n le nombre de cellules voules et seed la graine à utiliser pour l'aléatoire.
voronoi([1000,500],w=4,c=0,n=100,seed=1123); translate([1050,0,0]) voronoi([1000,500],w=5,c=120,n=12,seed=614); translate([0,-650,0]) voronoi([1000,500],w=3,c=1,n=200,seed=614); translate([1050,-650,0]) voronoi([1000,500],w=3,c=1,n=200,seed=615);
module voronoi(dim, w, c, n, seed){
fn=fn==undef?32:fn;
n=n==undef?100:n;
dim=dim==undef?[1000,500]:dim;
table=pointgrid([dim[0],dim[1]],n=n,seed=seed);
c=c==undef?0:c;
t=table[0][0]+table[0][1];
w=w==undef?1:w;
seed=seed==undef?1/fn*n*c/w:seed;
outline(w=w*2,t="in") square(dim);
difference(){
square(dim);
cnc(-c/2)
for (p=table){
intersection_for(p2=table){
if (p!=p2){
translate((p+p2)/2 -normal(p2-p)*w){
rotate([0,0,-myangle(p,p2)])
translate([-t,-t])
square([2*t, t]);
}}}}}}
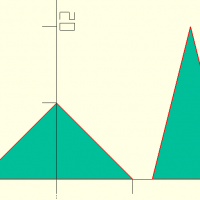
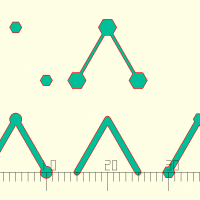
trace(table,d,dot,fn,dotfn,tr,d2)
abc=[[0,0],[sin(30)*10,cos(30)*10],[10,0]]; trace(abc); translate([15,0,0]) trace(abc,dot=false,fn=16); translate([30,0,0]) trace(abc,dot=true,dotfn=6); translate([0,15,0]) trace(abc, dot=true,dotfn=6,tr=false); translate([15,15,0]) trace(abc,d=0.5,dot=true,dotfn=6,tr=true,d2=3);
module trace(table,d,fn,dot,dotfn,tr,d2){
tr=tr==undef?true:tr;
fn=fn==undef?8:dot==true?4:fn;
dotfn=dotfn==undef?16:dotfn;
dot=dot==undef?true:dot;
d=d==undef?1:d;
d2=d2==undef?d*2:d2;
for(i=[0:len(table)-2]){
if(tr==true)
{
hull(){
translate(table[i])
circle(d=d,$fn=fn);
translate(table[i+1])
circle(d=d,$fn=fn);
}
}
if(dot==true){
translate(table[i]) circle(d=d2,$fn=dotfn);}
if(dot==true){
translate(table[i+1]) circle(d=d2,$fn=dotfn);}
}
}
outline(w,t)
abc=square([50,50],center=true); #translate([0,0,2]) 2D(abc); outline(w=3) 2D(abc); #translate([55,0,2]) 2D(abc); translate([55,0,0]) outline(w=3,t="in") 2D(abc); #translate([110,0,2]) 2D(abc); translate([110,0,0]) outline(w=3,t="out") 2D(abc);
module outline (w,t){
w=w==undef?1:w;
t=t==undef?"on":t;
difference()
{
offset(t=="out"?w:t=="in"?0:w/2)
children();
offset(t=="out"?0:t=="in"?-w:-w/2)
children();
}
}
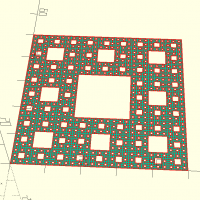
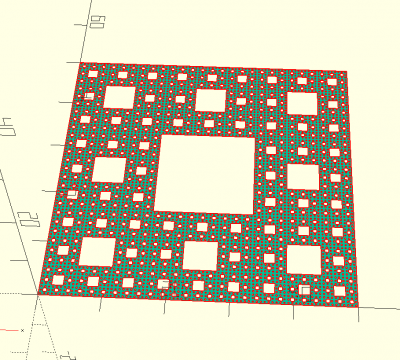
menger(d,maxit)
menger(d=50,maxit=5);
module menger(d,maxit,it){
let(it=it==undef?0:it)
if(it==maxit){
square([d,d]);
}
else{
union(){
menger(d=d/3+0.001,maxit=maxit,it=it+1);
translate([d/3,0])
menger(d=d/3+0.001,maxit=maxit,it=it+1);
translate([d/3*2,0])
menger(d=d/3+0.001,maxit=maxit,it=it+1);
translate([0,d/3])
menger(d=d/3+0.001,maxit=maxit,it=it+1);
translate([d/3*2,d/3])
menger(d=d/3+0.001,maxit=maxit,it=it+1);
translate([0,d/3*2])
menger(d=d/3+0.001,maxit=maxit,it=it+1);
translate([d/3,d/3*2])
menger(d=d/3+0.001,maxit=maxit,it=it+1);
translate([d/3*2,d/3*2])
menger(d=d/3+0.001,maxit=maxit,it=it+1);
}}}
Objets 3D
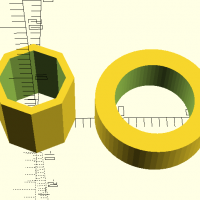
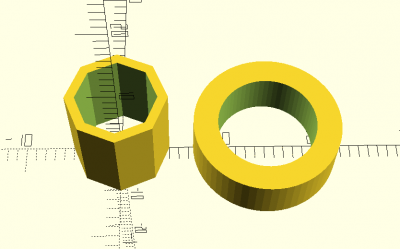
tube(d1,d2,h,center)
tube(d1=10,d2=8,h=10,$fn=8); translate([15,0,0]) tube(d1=15,d2=10,h=5,$fn=64);
module tube (d1,d2,h,center){
d1=d1==undef?10:d1;
d2=d2==undef?8:d2;
h=h==undef?30:h;
center=center==undef?false:center;
translate([0,0,center==true?-h/2:0])
difference(){
cylinder(d=d1,h=h);
translate([0,0,-1])
cylinder(d=d2,h=h+2);
}
}
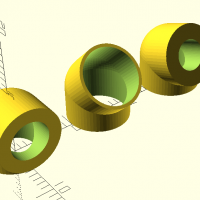
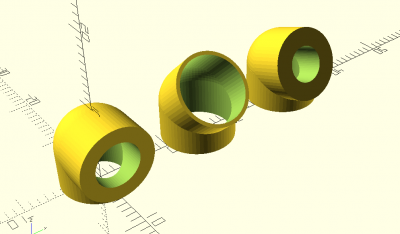
coude(d1,d2,a)
coude(d1=10,d2=6,$fn=64); translate([0,15,0]) coude(d1=10,d2=9,a=45,$fn=64); translate([0,30,0]) coude(d1=10,d2=5,a=67.5,$fn=64);
module coude(d1,d2,a){
d1=d1==undef?10:d1;
d2=d2==undef?8:d2;
a=a==undef?90:a<=-90?-90:a>=90?90:a;
difference(){
union(){
cylinder(d=d1,h=d1/2);
translate([0,0,d1/2])
sphere(d=d1);
translate([0,0,d1/2])
rotate([0,a,0])
cylinder(d=d1,h=d1/2);
}
union(){
translate([0,0,-1])
cylinder(d=d2,h=d1/2+1);
translate([0,0,d1/2])
sphere(d=d2);
translate([0,0,d1/2])
rotate([0,a,0])
cylinder(d=d2,h=d1/2+1);
}
}
}
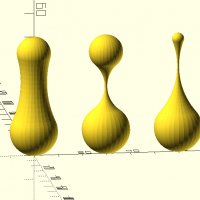
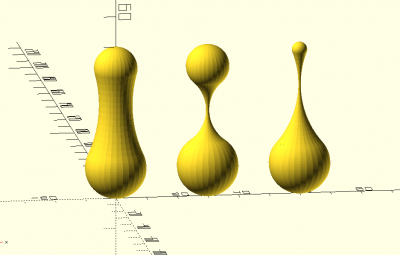
bone(h,d1,d2,c,q)
bone(h=50,d1=20,d2=14.14214,c=80,q=128); translate([30,0,0]) bone(h=50,d1=20,d2=14.14214,c=25,q=128); translate([60,0,0]) bone(h=50,d1=20,d2=5,c=60,q=128);
module bone(h,d1,d2,c,q){
h = h == undef ? 50 : h;
d1 = d1 == undef ? 20 : d1;
d2 = d2 == undef ? 14.14214 : d2;
c = c == undef ? 40 : c;
q = q == undef ? 128 : q;
rotate_extrude(){
rotate_extrude_correct(){
cnc((c)*2,$fn=q)
{
circle(d=d1,$fn=q);
translate([0,h])
circle(d=d2,$fn=q);
}
}
}
}
roundcube(s,b,t,center,q)
roundcube(); translate([65,0,0]) roundcube(s=[20,30,50], b=[2,4,6,8],t=[10,12,14,16],q=64); translate([95,0,0]) roundcube(s=[70,30,40], b=[5,5,5,5],t=[35,35,35,35],q=64);
module roundcube (s,b,t,center,q){
s=s==undef?[50,40,30]:s;
b=b==undef?[5,5,5,5]:b;
t=t==undef?[20,20,20,20]:t;
center=center==undef?false:center;
translate([center==true?-s[0]/2:0,center==true?-s[1]/2:0,center==true?-s[2]/2:0])
hull(){
translate([b[0]/2,b[0]/2,b[0]/2]) sphere(d=b[0]);
translate([s[0]-b[1]/2,b[1]/2,b[1]/2]) sphere(d=b[1]);
translate([s[0]-b[2]/2,s[1]-b[2]/2,b[2]/2]) sphere(d=b[2]);
translate([b[3]/2,s[1]-b[3]/2,b[3]/2]) sphere(d=b[3]);
translate([t[0]/2,t[0]/2,s[2]-t[0]/2]) sphere(d=t[0]);
translate([s[0]-t[1]/2,t[1]/2,s[2]-t[1]/2]) sphere(d=t[1]);
translate([s[0]-t[2]/2,s[1]-t[2]/2,s[2]-t[2]/2]) sphere(d=t[2]);
translate([t[3]/2,s[1]-t[3]/2,s[2]-t[3]/2]) sphere(d=t[3]);
}
}
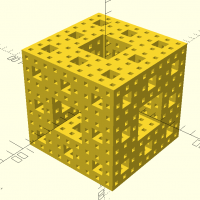
menger3D(d,maxit)
 Attention, la prévisualisation amène des erreurs d'affichage. Mais le résultat final est bon.
Attention, la prévisualisation amène des erreurs d'affichage. Mais le résultat final est bon.
menger3D(d=100,maxit=3);
module menger3d(it=1,d,maxit){
if (it==maxit){
cube([d,d,d],center=true);
}
if (it<=maxit){
union(){
for (i=[-1:1]){
translate([d/3,d/3,d/3*i]) rotate([0,90,0]) menger3d(it=it+1,d=d*1/3,maxit=maxit);
translate([-d/3,d/3,d/3*i]) rotate([0,90,0]) menger3d(it=it+1,d=d*1/3,maxit=maxit);
}
translate([0,d/3,d/3]) rotate([0,90,0]) menger3d(it=it+1,d=d*1/3,maxit=maxit);
translate([0,d/3,-d/3]) rotate([0,90,0]) menger3d(it=it+1,d=d*1/3,maxit=maxit);
for (i=[-1:1]){
translate([d/3,-d/3,d/3*i]) rotate([0,90,0]) menger3d(it=it+1,d=d*1/3,maxit=maxit);
translate([-d/3,-d/3,d/3*i]) rotate([0,90,0]) menger3d(it=it+1,d=d*1/3,maxit=maxit);
}
translate([0,-d/3,d/3]) rotate([0,90,0]) menger3d(it=it+1,d=d*1/3,maxit=maxit);
translate([0,-d/3,-d/3]) rotate([0,90,0]) menger3d(it=it+1,d=d*1/3,maxit=maxit);
translate([d/3,0,d/3]) rotate([0,90,0]) menger3d(it=it+1,d=d*1/3,maxit=maxit);
translate([d/3,0,-d/3]) rotate([0,90,0]) menger3d(it=it+1,d=d*1/3,maxit=maxit);
translate([-d/3,0,d/3]) rotate([0,90,0]) menger3d(it=it+1,d=d*1/3,maxit=maxit);
translate([-d/3,0,-d/3]) rotate([0,90,0]) menger3d(it=it+1,d=d*1/3,maxit=maxit);
}}}
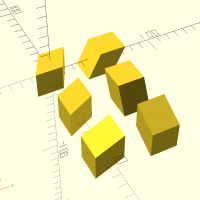
jcube(d,maxit)
jcube(d=100,maxit=4);
module jcube(it,d,maxit){
it=it==undef?1:it;
union()
{
if(it==maxit)
{
cube([d,d,d],center=true);
}
if(it<=maxit)
{
translate([d/2,d/2,d/2]) translate([-d/2*(sqrt(2)-1),-d/2*(sqrt(2)-1),-d/2*(sqrt(2)-1)]) jcube(it=it+1,maxit=maxit,d=d*(sqrt(2)-1));
translate([-d/2,d/2,d/2]) translate([d/2*(sqrt(2)-1),-d/2*(sqrt(2)-1),-d/2*(sqrt(2)-1)]) jcube(it=it+1,maxit=maxit,d=d*(sqrt(2)-1));
translate([d/2,-d/2,d/2]) translate([-d/2*(sqrt(2)-1),d/2*(sqrt(2)-1),-d/2*(sqrt(2)-1)]) jcube(it=it+1,maxit=maxit,d=d*(sqrt(2)-1));
translate([-d/2,-d/2,d/2]) translate([d/2*(sqrt(2)-1),d/2*(sqrt(2)-1),-d/2*(sqrt(2)-1)]) jcube(it=it+1,maxit=maxit,d=d*(sqrt(2)-1));
translate([d/2,d/2,-d/2]) translate([-d/2*(sqrt(2)-1),-d/2*(sqrt(2)-1),d/2*(sqrt(2)-1)]) jcube(it=it+1,maxit=maxit,d=d*(sqrt(2)-1));
translate([-d/2,d/2,-d/2]) translate([d/2*(sqrt(2)-1),-d/2*(sqrt(2)-1),d/2*(sqrt(2)-1)]) jcube(it=it+1,maxit=maxit,d=d*(sqrt(2)-1));
translate([d/2,-d/2,-d/2]) translate([-d/2*(sqrt(2)-1),d/2*(sqrt(2)-1),d/2*(sqrt(2)-1)]) jcube(it=it+1,maxit=maxit,d=d*(sqrt(2)-1));
translate([-d/2,-d/2,-d/2]) translate([d/2*(sqrt(2)-1),d/2*(sqrt(2)-1),d/2*(sqrt(2)-1)]) jcube(it=it+1,maxit=maxit,d=d*(sqrt(2)-1));
translate([-d/2,-d/2,0]) translate([d/2*(1-(2*(sqrt(2)-1))),d/2*(1-(2*(sqrt(2)-1))),0]) jcube(it=it+1,maxit=maxit,d=d*(1-(2*(sqrt(2)-1))));
translate([-d/2,d/2,0]) translate([d/2*(1-(2*(sqrt(2)-1))),-d/2*(1-(2*(sqrt(2)-1))),0]) jcube(it=it+1,maxit=maxit,d=d*(1-(2*(sqrt(2)-1))));
translate([d/2,-d/2,0]) translate([-d/2*(1-(2*(sqrt(2)-1))),d/2*(1-(2*(sqrt(2)-1))),0]) jcube(it=it+1,maxit=maxit,d=d*(1-(2*(sqrt(2)-1))));
translate([d/2,d/2,0]) translate([-d/2*(1-(2*(sqrt(2)-1))),-d/2*(1-(2*(sqrt(2)-1))),0]) jcube(it=it+1,maxit=maxit,d=d*(1-(2*(sqrt(2)-1))));
translate([-d/2,0,-d/2]) translate([d/2*(1-(2*(sqrt(2)-1))),0,d/2*(1-(2*(sqrt(2)-1)))]) jcube(it=it+1,maxit=maxit,d=d*(1-(2*(sqrt(2)-1))));
translate([-d/2,0,d/2]) translate([d/2*(1-(2*(sqrt(2)-1))),0,-d/2*(1-(2*(sqrt(2)-1)))]) jcube(it=it+1,maxit=maxit,d=d*(1-(2*(sqrt(2)-1))));
translate([d/2,0,-d/2]) translate([-d/2*(1-(2*(sqrt(2)-1))),0,d/2*(1-(2*(sqrt(2)-1)))]) jcube(it=it+1,maxit=maxit,d=d*(1-(2*(sqrt(2)-1))));
translate([d/2,0,d/2]) translate([-d/2*(1-(2*(sqrt(2)-1))),0,-d/2*(1-(2*(sqrt(2)-1)))]) jcube(it=it+1,maxit=maxit,d=d*(1-(2*(sqrt(2)-1))));
translate([0,-d/2,-d/2]) translate([0,d/2*(1-(2*(sqrt(2)-1))),d/2*(1-(2*(sqrt(2)-1)))]) jcube(it=it+1,maxit=maxit,d=d*(1-(2*(sqrt(2)-1))));
translate([0,-d/2,d/2]) translate([0,d/2*(1-(2*(sqrt(2)-1))),-d/2*(1-(2*(sqrt(2)-1)))]) jcube(it=it+1,maxit=maxit,d=d*(1-(2*(sqrt(2)-1))));
translate([0,d/2,-d/2]) translate([0,-d/2*(1-(2*(sqrt(2)-1))),d/2*(1-(2*(sqrt(2)-1)))]) jcube(it=it+1,maxit=maxit,d=d*(1-(2*(sqrt(2)-1))));
translate([0,d/2,d/2]) translate([0,-d/2*(1-(2*(sqrt(2)-1))),-d/2*(1-(2*(sqrt(2)-1)))]) jcube(it=it+1,maxit=maxit,d=d*(1-(2*(sqrt(2)-1))));
}}}
Modificateurs formes 2D et 3D
ring(d,n)
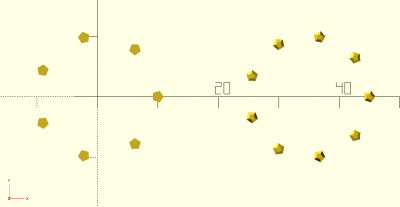 Fonctionne pour les objets 2D et 3D :
Fonctionne pour les objets 2D et 3D :
ring(d=20,n=7) circle(); translate([25,0,0]) ring(d=20,n=9) sphere();
module ring(d,n){
d=d==undef?10:d;
n=n==undef?5:n;
for(i=[0:n-1]){
rotate([0,0,360/n*i]){
translate([d/2,0,0])
children();
}
}
}
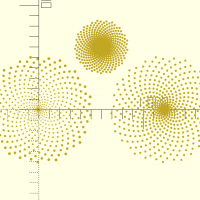
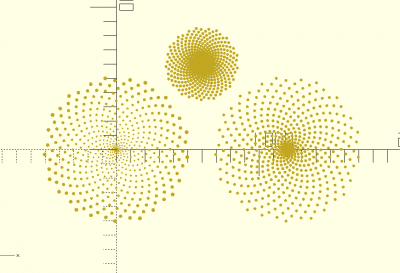
fibo(s,n,r)
fibo(s=1,n=512,r=true) circle(d=5); translate([1200,0,0]) fibo(s=1,n=512,r=false) circle(d=20); translate([600,600,0]) fibo(s=0.5,n=512,r=false) circle(d=20);
module fibo(s,n,r){
r=r==undef?true:r;
s=s==undef?1:s;
n=n==undef?128:n;
for(i=[1:n]){
rotate([0,0,angledor*i])
translate([s*i,0,0])
scale(r==true?s+pow(1.003,i):1)
children();
}
}
cnc(d,show)
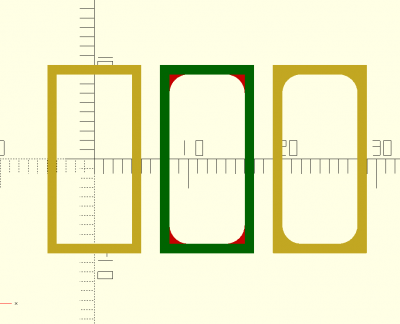 Simule l'utilisation d'une CNC où d est le diamètre de la mèche.
Simule l'utilisation d'une CNC où d est le diamètre de la mèche.
show=true/false permet de voir “ce que donne” la différence entre la forme originelle et celle qui serait coupée à la CNC.
difference(){
square([10,20],center=true);
square([8,18],center=true);
}
translate([12,0,0])cnc(d=4,show=true){
difference(){
square([10,20],center=true);
square([8,18],center=true);
}}
translate([24,0,0])cnc(d=4,show=false){
difference(){
square([10,20],center=true);
square([8,18],center=true);
}}
module cnc(d,show){
show=show==undef?false:show;
d = d == undef ? 3:d;
if(show==false){
offset(-d/2,$fn=32)
offset(d/2,$fn=32)
children();
}
else
{
color("green")
linear_extrude(1)
children();
color("red")
linear_extrude(0.5)
difference()
{
offset(-d/2,$fn=32)
offset(d/2,$fn=32)
children();
children();
}
}
}
chull(m)
chull(m=true){
sphere(d=1,$fn=16);
translate([10,10,00]) sphere(d=1,$fn=16);
translate([20,0,00]) sphere(d=1,$fn=16);
translate([30,0,00]) sphere(d=1,$fn=16);
translate([30,-10,00]) sphere(d=1,$fn=16);
translate([0,-10,00]) sphere(d=1,$fn=16);
}
translate([0,-25,0]) chull(m=false){
sphere(d=1,$fn=16);
translate([10,10,00]) sphere(d=1,$fn=16);
translate([20,0,00]) sphere(d=1,$fn=16);
translate([30,0,00]) sphere(d=1,$fn=16);
translate([30,-10,00]) sphere(d=1,$fn=16);
translate([0,-10,00]) sphere(d=1,$fn=16);
}
module chull(m){
union()
for(i=[0:$children-2]){
hull(){
children(m==true?0:i);
children(i+1);
}
}
}
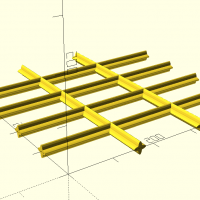
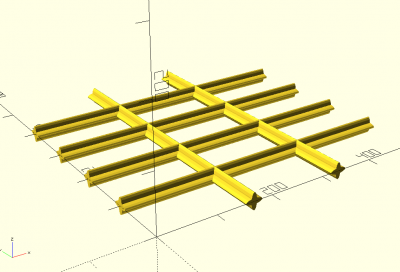
grid(dim,x,y)
grid([500,500],x=3,y=5){
ellipse([10,30]);
ellipse([30,10]);
}
module grid (dim,x,y){
dim=dim==undef?[100,100]:dim;
x=x==undef?10:x;
y=y==undef?10:y;
for(i=[1:x-1])
translate([i*dim[0]/x,0,0])
rotate([-90,0,0])
linear_extrude(dim[1])
children();
for(i=[1:y-1])
translate([0,i*dim[1]/y,0])
rotate([-90,0,-90])
linear_extrude(dim[0])
children();
}
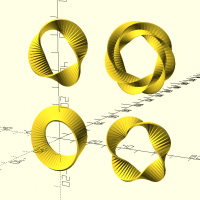
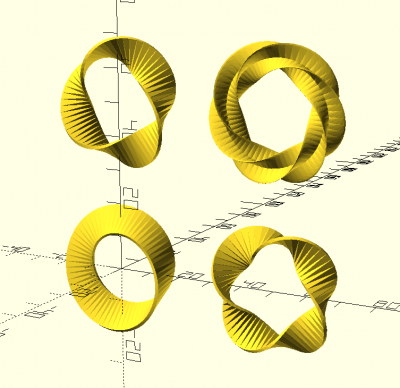
moebius(d,t,fn)
moebius(fn=64){
square([1,10],center=true);}
translate([50,0,0]) moebius(fn=64,t=2){
square([1,10],center=true);}
translate([0,0,50]) moebius(fn=64,t=1.5){
square([1,10],center=true);}
translate([50,0,50]) moebius(fn=64,t=1.5){
ellipse([1,10]);
ellipse([10,1]);}
module moebius(d,t,fn){ // version 2.0
fn = fn == undef ? 128 :fn;
d = d == undef ? 30 :d;
t = t == undef ? 0.5 :t;
union(){
for(j=[0:$children-1])
{
for(i=[1:fn]){
hull(){
rotate([0,360/fn*i,0])
translate([d/2,0,0])
rotate([0,0,i*(360*t)/fn])
linear_extrude(0.1)
children(j);
rotate([0,360/fn*(i+1),0])
translate([d/2,0,0])
rotate([0,0,(i+1)*(360*t)/fn])
linear_extrude(0.1)
children(j);
}
}
}
}
}
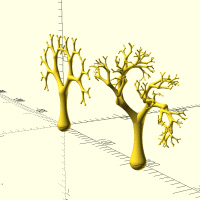
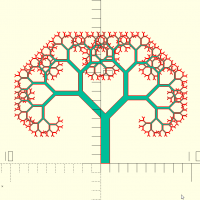
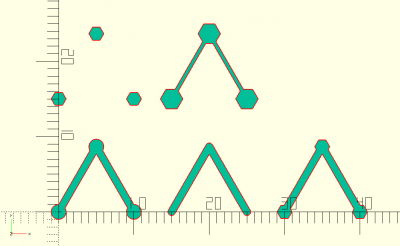
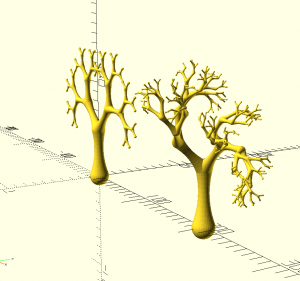
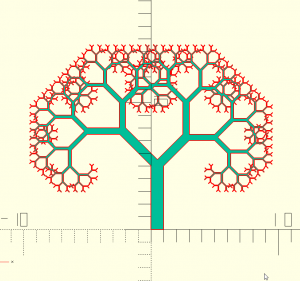
pythatree(a,h,sp,maxit,b,r1,r2,s,d)
pythatree(d="z",h=50,maxit=5,r1=0,r2=0) bone(h=50,d1=20,d2=14.14214,c=160,$fn=32); translate([200,0,0])pythatree(d="z",h=50,maxit=7,r1=0,r2=90) bone(h=50,d1=20,d2=14.14214,c=160,$fn=32);
pythatree(d="y",h=5,maxit=9) square([1,5]);
module pythatree (a,h,sp,maxit,b,r1,r2,s,d){
a = a == undef ? 45 : a;
h = h == undef ? 1 : h;
sp = sp == undef ? 0 : sp;
maxit = maxit == undef ? 3 : maxit;
b = b == undef ? 1 : b;
r1 = r1 == undef ? 0 : r1;
r2 = r2 == undef ? 0 : r2;
s = s == undef ? py : s;
d = d == undef ? "y" : d;
children();
if(b<=maxit)
{
translate([d=="x"?h:d=="y"?sp:-sp, d=="x"?-sp:d=="y"?h:0, d=="x"?0:d=="y"?0:h])
rotate([d=="x"?0:d=="y"?r2:0, d=="x"?r2:d=="y"?0:-a, d=="x"?-a:d=="y"?-a:r2])
scale([s,s,s])
pythatree(a=a,h=h,sp=sp,maxit=maxit,b=b+1,r1=r1,r2=r2,s=s,d=d)
{
children();
};
translate([d=="x"?h:d=="y"?-sp:sp, d=="x"?sp:d=="y"?h:0, d=="x"?0:d=="y"?0:h])
rotate([d=="x"?0:d=="y"?r1:0, d=="x"?r1:d=="y"?0:a, d=="x"?a:d=="y"?a:r1])
scale([s,s,s])
pythatree(a=a,h=h,sp=sp,maxit=maxit,b=b+1,r1=r1,r2=r2,s=s,d=d)
{
children();
};
}
}
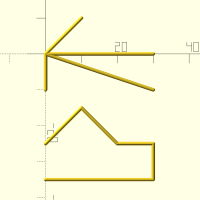
mirror(a,x,y)
abc=chaincurve(center(LetterL),3); 2D(abc); translate([60,0,0]) 2D(mirror(abc,x=true)); translate([0,-80,0]) 2D(mirror(abc,y=true)); translate([60,-80,0]) 2D(mirror(abc,x=true,y=true));
function mirror(a,x,y)=let(
xx=x==undef?1:x==true?-1:1,
yy=y==undef?1:y==true?-1:1,
aa=[
for(i=[0:len(a)-1])
each
[
[a[i][0]*xx,a[i][1]*yy]
]
]
)aa;
translate3D(a,b) & rescale3D(a,b)
abc=cube([10,10,10],center=true); def=translate3D(rescale3D(abc,2),[10,20,30]); 3D(abc); 3D(def);
function translate3D(a,b)=[[for(i=[0:len(a[0])-1]) a[0][i]+b],a[1]]; function rescale3D(a,s)= [[for(i=[0:len(a[0])-1]) a[0][i]*s],a[1]];
skew(XY,XZ,YX,YZ,ZX,ZY)
skew(XY=0.5) cube([25,25,25],center=true); translate([50,0,0]) skew(XZ=0.5) cube([25,25,25],center=true); translate([0,-50,0]) skew(YX=0.5) cube([25,25,25],center=true); translate([50,-50,0]) skew(YZ=0.5) cube([25,25,25],center=true); translate([0,-100,0]) skew(ZX=0.5) cube([25,25,25],center=true); translate([50,-100,0]) skew(ZY=0.5) cube([25,25,25],center=true);
module skew(XY,XZ,YX,YZ,ZX,ZY){
matrice=[
[1,XY,XZ,0], //[redimX, skewXY, skewXZ,translateX]
[YX,1,YZ,0], //[SkewYX,RedimY,SkewYZ,translateY]
[ZX,ZY,1,0] //[SkewZX, SkewZY,redimZ,TranslateZ]
];
multmatrix(matrice){
children();
}
}
2D vers 3D
simple3D(a,b,h,angle,correct)
abc=ngon(d=50,fn=3); def=chaincurve(koch(abc,maxit=2)); my3Dobject=simple3D(abc,def,h=70); 3D(my3Dobject);
function simple3D(a,b,h,bottom,top,angle,correct) = let (
angle=angle==undef?0:angle,
correct=correct==undef?0:correct,
bottom=true,
top=true,
c=2Drot(interpolate(L1,L2,maxstep=1,step=0,correct=correct,q=1),angle),
d=2Drot(interpolate(L1,L2,maxstep=1,step=1,correct=correct,q=1),angle),
aa=[ for(i=[0:len(c)]) each[[c[i][0],c[i][1],0],[d[i][0],d[i][1],h]] ],
bb=[ for(i=[0:1:len(aa)]) each [[i,i+1,i+2],[i+1,i+3,i+2]] ],
cc=bottom==true?[ for(i=[0:2:len(aa)]) each [i] ]:[],
dd=top==true?[ for(i=[0:2:len(aa)]) each [len(aa)-1-i] ]:[],
ee=concat(bb,[cc],[dd])
)
[clean(aa),clean(ee)];
2Dto3D(a,b,h,segment,correct)
 Attention : Ce module générera énormément d'erreurs mais le résultat final devrait être bon. a est la première forme. b est la seconde forme. h la hauteur de la forme. correct permet de corriger de quel point à quel point se fait le raccords afin d'éviter les rotations.
Attention : Ce module générera énormément d'erreurs mais le résultat final devrait être bon. a est la première forme. b est la seconde forme. h la hauteur de la forme. correct permet de corriger de quel point à quel point se fait le raccords afin d'éviter les rotations.
Ce module est sujet à beaucoup de bugs!!! Merci de préférer tant que maintenant le passage par la fonction simple3D()
Les autres variables seron documentées plus tard.
abc=ngon(d=40,fn=5); def=fractshape(d=40,fn=5,it=3,inside=true); ghi=chaincurve(def); 2Dto3D(abc,def,segment=4,h=20); translate([50,0,0]) 2Dto3D(abc,ghi,segment=8,h=20); translate([0,50,0]) 2Dto3D(circle(d=40,fn=16),square([20,20],center=true),h=20,segment=16,correct=0); translate([50,50,0]) 2Dto3D(circle(d=40,fn=16),square([20,20],center=true),h=20,segment=4,correct=6);
module 2Dto3D(a,b,h,segment,correct,quality,rotation){
angle=rotation==undef?0:rotation/segment;
quality=quality==undef?1:quality;
he=h==undef?64:h;
mm=segment==undef?16:segment;
aabc=a==undef?ngon(d=50,fn=3):a;
adef=b==undef?chaincurve(koch(ngon(d=50,fn=3),maxit=1),fn=4):b;
correct=correct==undef?0:correct;
union(){
for(i=[0:mm-1]){
my3Dobject=to3D(
2Drot(interpolate(aabc,adef,maxstep=mm,step=i,correct=correct,q=quality),i*angle),
2Drot(interpolate(aabc,adef,maxstep=mm,step=i+1,correct=correct,q=quality),(i+1)*angle),
h=he/mm,
top=i==mm-1?true:true,
bottom=i==0?true:true);
translate([0,0,i*he/mm])
color([1/mm*i,1-(1/mm*i),1,1])
union(){
polyhedron(my3Dobject[0],my3Dobject[1]);
polyhedron(my3Dobject[0],my3Dobject[1]);}
}
}
}